반응형
Wavelet Transform
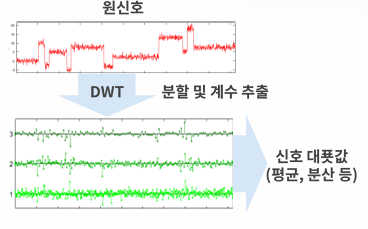
- wavelet 데이터를 밴드별로 분할시켜서 증폭시킴
- window length를 바꿔가며 STFT를 여러번 진행하는 개념
- 복잡한 주파수 특성을 가진 신호에 대해 다해상도 분석을 통해 주파수에 관한 정보 획득
→ 시간 분해능과 주파수 분해능을 모두 고려
(Wevelet Mother Function을 변화시켜 주파수 해상도나 시간 해상도를 조절)
장점
- FTF보다 적용범위가 넓음
- 특징요소 추출 자동화 용이
- 전처리 및 특징요소 추출 동시 수행
- 다수 신호에 대한 일괄적인 데이터 가공에 유리
단점
- 데이터 크기에 따라 추출 결과 변함
- 추출되는 특징요소 종류 많음

python 코드
모듈 import
import pandas as pd
import numpy as np
import scipy.stats as sp
!pip install PyWavelets
import pywt
데이터 불러오기
Data = pd.read_csv(My_path + 'ExampleData.csv', sep=',', header=None)
Data.shape→ (3000, 2)

시각화
plt.figure(figsize=(20,6))
plt.subplot(2,1,1) # x 방향 가속도 데이터
plt.plot(Data.iloc[:,0] , Data.iloc[:,1], color='r')
plt.ylabel('Acceleration (g)',fontsize=15, color='r')
plt.legend(['Acc_x'], loc = 'upper right')
plt.grid()
plt.show()

wavelet parameter 설정
8 레벨 지정
# Wavelet options
MotherWavelet = pywt.Wavelet('haar') # Mother wavelet (모함수) 지정
Level = 8 # Wavelet 분해 레벨 지정
select = 8 # 특징추출 영역 고주파 영역부터 개수 지정 (d1~)
wavelet 변환
Data_Target = Data.iloc[:,1] # 시계열 데이터 센서 종류 선택
Coefficient = pywt.wavedec(Data_Target, MotherWavelet, level=Level, axis=0) #9번 분해
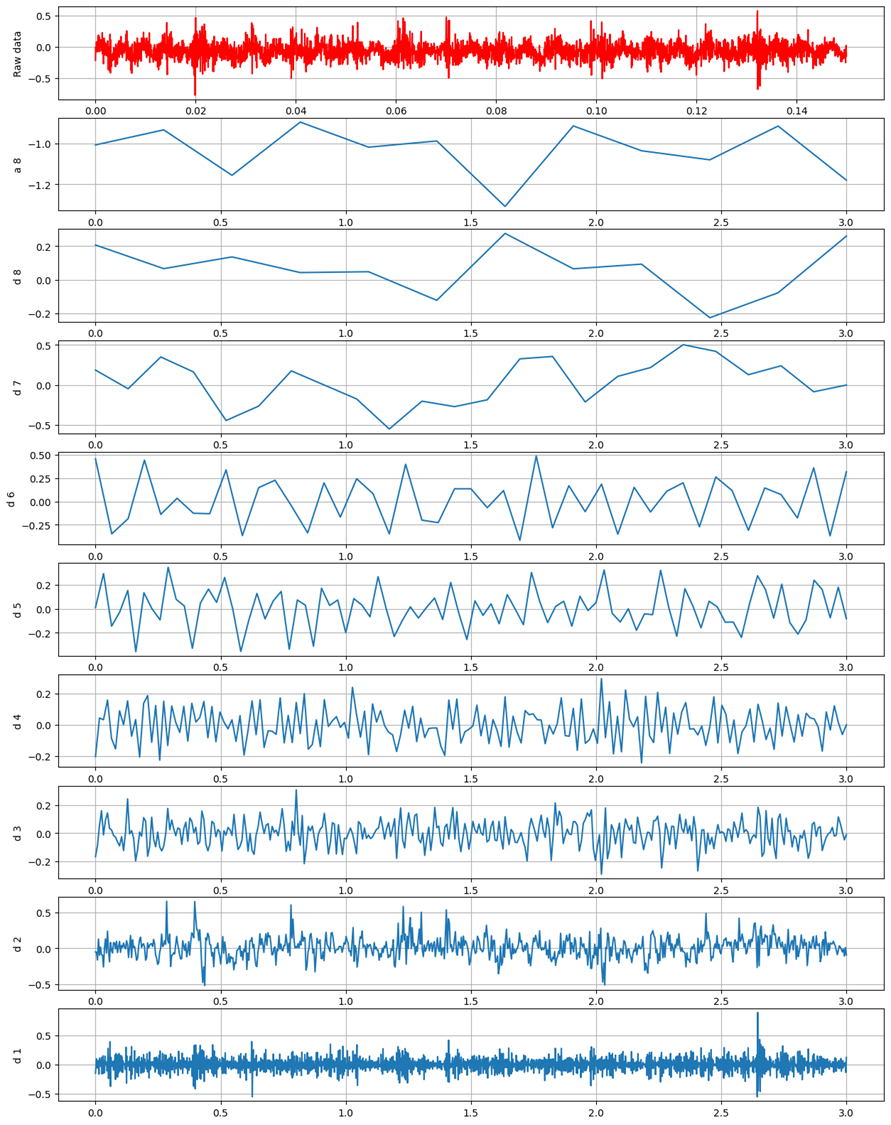
시각화
plt.figure(figsize=(15,20))
plt.subplot(Level+2,1,1)
plt.plot(Data.iloc[:,0], Data_Target, color='r')
plt.ylabel('Raw data')
plt.grid()
plt.subplot(Level+2,1,2)
Time_temp = np.arange( 0 , 3 + 3/(len(Coefficient[0])-1) , 3/(len(Coefficient[0])-1) )
plt.plot(Time_temp , Coefficient[0])
plt.ylabel('a %d' %(Level))
plt.grid()
plt.subplot(Level+2,1,3)
Time_temp = np.arange( 0 , 3 + 3/(len(Coefficient[0])-1) , 3/(len(Coefficient[0])-1) )
plt.plot(Time_temp , Coefficient[1])
plt.ylabel('d %d' %(Level))
plt.grid()
for k in range(2,Level+1):
plt.subplot(Level+2,1,k+2)
Time_temp = np.arange( 0 , 3 + 3/(len(Coefficient[k])-1) , 3/(len(Coefficient[k])-1) )
plt.plot(Time_temp , Coefficient[k])
plt.ylabel('d %d'%(Level+1-k))
plt.grid()
plt.show()
반응형
'개발기록 > python' 카테고리의 다른 글
| [python] 주파수 신호 분석 방법론 2 - STFT (Short Time Fourier Transform) (1) | 2024.11.25 |
|---|---|
| [python] 주파수 신호 분석 방법론 1 - FFT (Fast Fourier Transform) (0) | 2024.11.24 |
| [python] selenium-stealth 셀레늄 감지 방지 (구글 크롬) (1) | 2024.11.15 |
| 구글 코랩(Colab) 사용하기 (+구글 드라이브 연결, 압축풀기) (0) | 2024.11.07 |
| [python] Selenium 요소 클릭, 선택 (checkbox, radio button, select box) (0) | 2024.10.14 |




댓글